Showing posts with label education. Show all posts
Friday, January 31, 2020
Types of cables in guided media
Twisted-Pair cable
- It consists of four pairs of copper wires coated with an insulating materials like plastic or teflon and twisted together.
- It is often used data network for short and medium length connections because of it's relatively lower cost compared to optical fiber and co-axial cable.
- Twisted pair cables are of two types:
- Shielded twisted pair cable (STP)
- Shielded twisted pair cables (STP) is similar in construction to un-shielded twisted-pair cabled wire (UTP) except that twisted pair is enclose in a woven copper for providing extra protection from external interference.
- It is expensive then UTP.
- Transmission speed is upto 500 mbps at 100m range.
- Un-Shielded twisted pair cable (UTP)
- UTP cable consists of number of twisted pairs of wires with a simple plastic casing.
- It is commonly used in telephone line system.
- The commonly used UTP cable is Category 5 cable (Cat 5) which is used with fast ethernet.
Coaxial Cable
- A coaxial cable has a single inner conductors that transmits electric signals,the outer conductor act as a ground,the two conductors are separated by insulation.The inner conductor,insulator and the outer conductor are wrapped in a sheath of teflon or pvc.
- The copper wire is used for both inner and outer conductor,the signal is transmitted over the surface of inner conductors.
- A thicker coaxial cable can transmit more data than thinner one.
- The commonly used coaxial cable is telephone trunklines, broadband internet networking cables, high speed computer data busses, carrying cable television signals, and connecting radio transmitters and receivers to their antennas.
Optical Fiber
- Optical fiber, refers to the medium and the technology associated with the transmission of information as light pulses along a glass or plastic strand or fiber. A fiber optic cable can contain a varying number of these glass fibers -- from a few up to a couple hundred.
- It has high bandwidth and faster speed.
- It's flexibility is generally high.
- It helps in secure transmission process.
- It is commonly used in surgery and dentistry,lighting and decoration and mechanical inspections.
Number system || chapter two BCA TU || Digital logic
Number system
A number system in base r or radius r uses unique symbols for r digits. One or more digits are combined to get a number.In computers, we are concerned with four kinds of number systems, as follows:
Decimal Number System ------------ Base 10
Binary Number System ------------ Base 2
Octal Number System ------------ Base 8
Hexa-Decimal Number System -------- Base 16
Decimal Number System
It consists of 10 digits (0-9).
Binary Number System
It consists of 2 digits (0-1).
Octal Number System
It consists of 8 digits (0-7).
Hexa-Decimal Number System
It consists of 16 digits (0-9 and A-E) whereas from digit 10 it is named after alphabets A that means A is number 10 and E is number 15.
Conversion of Decimal to Binary, Octal, Hexa-decimal
binary-divide by 2, for fraction multiply by 2
octal-divide by 8, for fraction multiply by 8, and,
hexadecimal-divide by 16, for fraction by 16.
Conversion of Binary to Decimal, Octal, Hexadecimal
decimal-multiply by 2 with the power of their descending position and for fraction with power of their ascending position but with negative sign in powers.
octal-multiply by 8 with the power of their position and for fraction with the power of negative sign.
hexadecimal-multiply 16 with the power in it and negative for fraction.
Conversion of Binary to Octal, Hexa-Decimal
8= that means while converting binary digits to octal we have to arrange three digits of binary number starting from last position to get octal number.
16= that means while converting binary digits to hexadecimal we have to arrange four digits of binary number starting from last position to get octal number.
Conversion of Octal, Hexadecimal to Binary
As said above each number of octal number equals to three digits of binary number i.e. final binary number will be combination of each number formed while converting.
Convert each hexadecimal digit to four digits of binary number and the combination of all digits will be the final conversion.
Radix Complement
The r's complement of "n" digit, number "N" in base "r" is defined as -N for N=0 and 0 for N=0.
Comparing with (r-1)'s complements the r's complement is obtained by adding 1 to the (r-1)'s complement since -N= [(-1)-N] +1.
Binary Arithmetic
Binary Addition
Binary Subtraction
Binary Multiply
Binary Divide
Binary Addition
The Addition of the Binary numbers involve the following steps:
Start addition by adding the bits in unit column (the right-most column).
The result of adding of a column is a sum with or without a carry.
Write the sum in the result of that column.
If a carry is present, the carry is carried over to the addition of the next left column.
Binary Subtraction
The steps for performing subtraction of the binary numbers are as follows: -
Start subtraction by subtracting the bit in the lower row from the upper row, in the unit column.
Use the binary subtraction rules. If the bit in upper row is less than lower row, borrow 1 from the upper row of the next column (on the left side).
Rule of subtraction
1-1=0 0-1=1 (borrowed 1 from upper one)
Binary Multiply
Rules for Binary Multiply: 1*0=0 1*1=1
Binary Division
Binary number is divided same as dividing decimal number.
Binary Coded Decimal (BCD)
In this code each digit is responsible by a 4-bit binary number. The positional weight is assigned to the binary digits in BCD code are 8-4-2-1 with 1 corresponding to LSB and corresponding MSB.
Positional 8 4 2 1
Weight
While converting from BCD to binary, convert same as converting binary.
0 1 2 3 4 5 6 7 8 9
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
Invalid BCD Codes
with 4-bits we can represent total 16 numbers (0000 to 1111) in BCD only first ten codes on used (0000 to 1001)
Therefore, remaining six-codes (1010 to 1111) are invalid in BCD.
The binary coding schemes that are mostly used are: -
Extended Binary Code Decimal Interchange Code (EBCDIC)
American Standard Code for Information Interchange (ASCII)
Unicode
EBCDIC
The Extended Binary Coded Decimal Interchange Code (EBDIC) uses 8 bits (4 bits for zone, 4 bits for digit) to represent a symbol in the data.
EBCDIC allows = 256 combinations of bits.
256 unique symbols are represented using EBCDIC code. It represents decimal numbers (0-9) lower case letters (a-z), upper case letters (A-Z), Special characters, and Control characters (printable and non-printable, e.g., for cursor movement, printer vertical spacing, etc.
EBCDIC codes are mainly used in the mainframe computers.
ASCII
The American Standard Code for Information interchange (ASCII) is widely used in computers of all types.
ASCII codes are two types- ASCII-7 and ASCII-8.
ASCII-7 is a 7-bit standard ASCII code. In ASCII-7, the first 3 bits are the zone bits and the next 4 bits are for the digits. ASCII-7 allows = 128 combinations. 128 unique symbols are represented using ASCII-7 has been modified by IBM to ASCII-8
ASCII-8 is an extended version of ASCII-7. ASCII-8 allows =256 combinations. ASCII-8 represents unique symbols. ASCII-8 is an 8-bit code having 4 bits for zone and 4 bits for the digits. ASCII is widely to represent data in computers.
Code 0-31 used for actions like Carriage Return (CR), Bell (BEL), etc.
Code 48-57 for numeric
Code 65-90 for uppercase letters
Code 97-122 for lowercase letters
Code 128-255 are extended ASCII codes.
Unicode
It is a universal character encoding standard for the representation of text which includes letters, numbers and symbols in multi-lingual environments. The Unicode Consortium based in California developed the Unicode standard.
It uses 32 bits to represent a symbol in the data.
It allows =4164895296 (~ 4 billion) combinations.
It can uniquely represent any character or symbol present in any language. In addition to the letters; mathematical and scientific symbols are also represented in Unicode.
It is compatible with the ASCII-8 codes. the first 256 codes are identical to the ASCII-8 codes.
Gray Code
It is also known as Reflected Binary Code is defined as an ordering of the binary number system such that each incremental value can only differ by one bit. I n gray code, whole traversing from one step to another step only one bit in the group changes. That is to say that two adjacent code numbers differ from each other by only one bit.
Gray code is the most popular of the unit distance code, but it is not applicable for Arithmetic Operations. Gray Code has some application is Analog to digital Convertors, as well as used for error correction in Digital Communication.
Excess-3 Code
It is basically a binary code which is made by adding 3 with equivalent decimal of binary number and again converting it into binary number. So, if we consider any binary number we have to first convert it into decimal number then add 3 with it and then convert into binary.
Self-complementing Property:
Excess-3 code is non-weighted and self-complementary code. A self-complementary binary code is always complemented themselves. The compliment of a binary number can be obtained from that number by replacing 0's with 1's and 1's with 0's. The sum of binary number and its complement is always equal to decimal 9. In other words, the 1's complement of an excess-3 code is the excess-3 code for the 9's complement of the corresponding decimal number.
Alpha-numeric Codes
A binary bit can represent only two symbols '0' and '1'. But it is not enough for communication between two computers because there we need many more symbols for communication.
These symbols are required to represent:
26 numbers with capital and small letters
Number 0 to 9
Punctuation marks
Alpha-numeric codes represent numbers and alphabetic characters. They also represent other characters such as punctuation symbols and instructions for conveying information.
Boolean algebra and logic gates
The most common postulates used to formulate various algebraic structures are:
Associative law: A binary operator * on a set S is said to be associative whenever:
(x*y) *z=x*(y*z)
Commutative law: A binary operator * on a set S is said to be commutative whenever:
x*y=y*x
Identity element: A set S is said to have an identity element with respect to a binary operation * on S if there exists an element eS with the property:
e*x=x*e=x for every xS
Inverse: A set having the identity element e with respect to a binary operator * is said to have an inverse whenever, for every xS, there exists an element yS such that:
x*y=e
Distributive law: If * and · are two binary operators on set S, * is said to be distributive over* whenever:
x*(y*z) =(x*y) *(y*z)
Theorem 1(a): x+x=x
Theorem 1(b):x*x=x
Theorem 2(a):x+1=x
Theorem 2(b):x*0=0
Theorem 3 :(x') '=x
Theorem 6(a):x+yx=x
Theorem 6(b):x(y+x)=x
Wednesday, January 29, 2020
Transmission media and it's types (TU BCA NOTES)
Transmission Media
- Transmission media the pathway network entities used to connect each other.
- Computer transmission media includes
- guided media
- unguided media
- Guided media transmits signals by sending electricity or light over a cable or wire
- It uses a cabling system that guides the data signals along a specific path.
- The data signals are bounded by the cabling system so it is also called bounded media.
- Examples:twisted-pair wire,co-axial cable,fiber optics cable.

- Un-guided transmission media consists of a means for the data signals to travel but nothing to guide that along a specific path.
- It transmits data through the open air.
- Examples: radio waves ,infrared signals and earth and satellite based microwaves.
Tuesday, January 28, 2020
What is K-MAP and how to solve it|| KARNAUGH MAP || BCA TU NEPAL || Digital Logic ||
Karnaugh Map (K-MAP)
The K-MAP is a graphical representation that provides a systematic method for simplifying a boolean expression.
Two Variable K-MAP
For n variable k-map 2^n cells are required.Therefore for two variable k-map,2^2=4 cells are required.
 |
For constructing three variable k-map 2^3=8 cells are required.
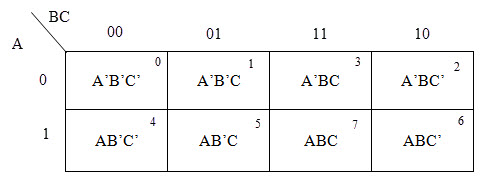
Four Variable K-MAP
For constructing four variable k-map 2^4=16 cells are required.
Why are K-MAPS used in boolean algebra?
Karnaugh's map are used to simplify real-world logic requirements so that they can be implemented using a minimum number of physical logic gates.K-MAP reduces the need for extensive calculations by taking advantage of human's pattern recognition capability
Grouping of cells for simplification in K-MAP
Adjacent cell's which have 1's can be grouped together in 2^n powert that is:
Two adjacent cells can be grouped together
Four adjacent cells can be grouped together
Eight adjacent cells can be grouped together
Sixteen adjacent cells can be grouped together
Rules followed for K-MAP simplification
So,these are the basic information about karnaugh's map if you have any problems or confusions regarding the topic feel free to contact us.
Subscribe to:
Comments
(
Atom
)